W rozdziale jest przedstawiona analiza opłacalności stosowania metodyki “Extreme Programming”. Przeprowadzona analiza będzie posługiwała się przygotowanymi we własnym zakresie modelami ekonomicznymi opisującymi proces budowy systemu informatycznego. W szczególności wykazana zostanie przewaga metodyki wynikająca z iteracyjności procesu wytwarzania oprogramowania, szybkiej implementacji funkcji o największej wartości oraz z elastyczności procesu produkcji.
Spis treści
- Ekonomiczna ocena metodyki “Extreme Programming”
- Wstęp
- Najważniejsze zasady “Extreme Programming”
- Fundamentalne wartości
- Stosowane praktyki
- Cykl życia oprogramowania
- Założenia upraszczające
- Analiza opłacalności podziału systemu na fragmenty
- Efekty szybkiej implementacji funkcji o największej wartości
- Wartość elastyczności procesu produkcji
- Zakończenie
- Bibliografia
Wstęp#
Burzliwy rozwój nowych narzędzi programistycznych oraz coraz bardziej zmienne otoczenie powodują ciągłą potrzebę dostosowywania metodologii tworzenia systemów informatycznych do nowych uwarunkowań. Mimo szeroko prowadzonych badań w tym zakresie wciąż nie udaje się jednak opracować panaceum na ogromne trudności zespołów programistycznych w dostarczeniu na czas produktu spełniającego wymagania klienta, jednocześnie nie przekraczając założonego budżetu. Te właśnie problemy stały się punktem wyjścia metodyki “Extreme Programming” opracowanej w latach dziewięćdziesiątych przez Kenta Becka, Warda Cunninghama i Rona Jeffrisa. Zaproponowali oni całkowicie nowe podejście do tworzenia oprogramowania akceptując prawo klienta do zmiany wymagań. Założenia leżące u podstaw tej metodyki okazały się w praktyce bardzo skuteczne co potwierdziły prace wdrożeniowe w takich przedsiębiorstwach jak Bayerische Landesbank, Credit Swiss Life, DaimlerChrysler, First Union National Bank, Ford Motor Company czy UBS [6]. Celem tej pracy będzie analiza czynników odpowiedzialnych za efektywność metodologii “Extreme Programming” oraz zbadanie jej ograniczeń. Autor postara się więc odpowiedzieć na pytanie, w jakich warunkach metodyka ta stanowi korzystną alternatywę wobec klasycznych metod (model kaskadowy). Przedstawiona analiza przeprowadzona zostanie z punktu widzenia odbiorcy produktu programistycznego, zaniedbane natomiast zostaną czynniki pozaekonomiczne wynikające z różnej organizacji procesu budowy oprogramowania. Z tego też względu celem rozdziału nie jest modelowanie konkretnych typów projektów, ale stworzenie modelu ogólnego pozwalającego na znalezieniu ekonomicznych przyczyn efektywności metodyki XP.
Najważniejsze zasady “Extreme Programming”#
Fundamentalne wartości#
Metodyka Extreme Programming opiera się na następujących wartościach, leżących u podstaw wszystkich wykonywanych czynności [2]: Komunikacja, Prostota, Sprzężenie zwrotne, Odwaga.Wartości te łączy ze sobą efekt synergii, u podstaw którego leży dążenie do szybkiego dostarczenia dobrej jakości oprogramowania zgodnego z oczekiwaniami klienta. Prosty produkt umożliwia łatwą komunikację, gdyż programiści nie mają problemu z rozszyfrowaniem sposobu jego działania. Wszechogarniająca komunikacja umożliwia natychmiastowe sprzężenie typu oczekiwania klienta – system informatyczny – świat rzeczywisty. Odwaga natomiast sprawia, że praca posuwa się szybko, a nowe problemy i zmieniające się wymagania nie spowalniają pracy zespołu.
Stosowane praktyki#
Z przytoczonych tu wartości wyprowadzić można dwanaście praktyk w trzech grupach, które stanowią fundament Extreme Programming [10]:Zasady oddziałujące na sposób kodowania dotyczą specyficznego dla XP stylu programowania, który może być stosowany również przez pojedynczych programistów. Stanowi to najbardziej wewnętrzną warstwę metodyki, na której budowane są dwie następne celem maksymalizacji efektów. Do tej kategorii zaliczamy:
- Testowanie – programiści tworzą testy wszystkich modułów, klient tworzy testy funkcjonalności
- Prosty projekt – projekt jest zrozumiały dla programistów i łatwy do zmiany
- Refactoring – system podlega ciągłej ewolucji poprzez przekształcanie istniejącego kodu, przy zapewnieniu zgodności z wszystkimi testami
- Ciągła integracja – nowy kod jest integrowany z istniejącym systemem zaraz po jego napisaniu i przetestowaniu
Zachowania zespołowe ustalają sposób współpracy i komunikacji w zespole. One to decydują o tym, że możliwa jest wydajna praca całego zespołu nad wspólnym projektem. Należą do nich:
- Programowanie w parach – cały kod produkcyjny jest tworzony przez dwuosobowe zespoły pracujące wspólnie przy jednym komputerze
- 40-godzinny tydzień pracy – dłuższy czas pracy oznacza spadek produktywności
- Wspólna własność kodu – każdy programista może poprawić każdy fragment kodu przy zachowaniu zgodności z testami
- Standardy programowania – kod napisany przez różnych programistów w zespole wygląda tak samo.
- Metafora (systemu) – kształt systemu jest określany przez porównanie do idei opisującej jego działanie.
Współpraca z klientem stanowi najbardziej zewnętrzną warstwę metodyki. Określa ona sposób dostarczenia klientowi systemu, który spełnia jego oczekiwania. Należy tu wymienić:
- Klient na miejscu – klient przebywa z zespołem programistycznym przez cały czas trwania projektu
- Dostarczanie zrealizowanego fragmentu systemu w krótkich odstępach czasu – program jest dostarczany klientowi przed rozwiązaniem całego problemu biznesowego
- Planowanie – klient decyduje o zakresie i czasie dostarczenia fragmentu systemu w oparciu o szacunki programistów.
Cykl życia oprogramowania#
Obok zasad dotyczących sposobu, programowania, zachowań zespołowych oraz współpracy z klientem niezwykle istotnym elementem metodyki XP jest proces wytwarzania oprogramowania. Łączy on wszystkie poprzednio opisane czynniki w jedną całość, zapewniając tym samym ich jak najlepsze współdziałanie. Proces ten przedstawiony jest na rysunku 1 [5].Pierwszym etapem rozpoczynającym prace nad tworzonym systemem jest analiza wstępna. Nie jest ona co prawda explicite uwzględniana przez twórców metodyki, jednak każde przedsięwzięcie powinno być poprzedzone strategiczną fazą oceny opłacalności i możliwości implementacji [13]. W okresie tym następują intensywne negocjacje z klientem mające na celu wypracowanie korzystnego dla obu stron kontraktu. Ze strony firmy programistycznej jej pracownicy próbują ogólnie uchwycić całość systemu oraz najważniejsze zadania przed nim stawiane. Efektem tego jest wybór środowiska implementacji, narzędzi CASE oraz ewentualnie zdecydowanie się na współpracę z innymi producentami lub zewnętrznymi ekspertami. Następne decyzje będące następstwem wstępnego rozeznania powinny określać planowane nakłady będące funkcją zaangażowanych zasobów takich jak pracownicy, oprogramowanie, sprzęt.
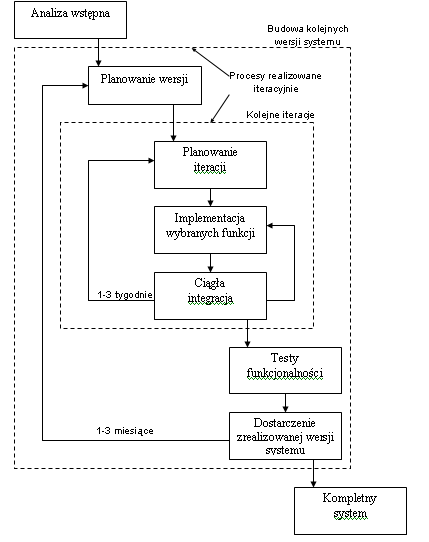
Ponieważ przedmiotem zainteresowania są na ogół bardzo zmienne wymagania i warunki zewnętrzne, nie próbuje się najczęściej dokładnie szacować całkowitych kosztów systemu (przy rutynowych zadaniach i stabilnych wymaganiach częściej stosuje się model kaskadowy). Zamiast tego szacuje się natomiast koszt pracy zespołu i to właśnie jest ujęte w kontrakcie [1]. Jeżeli klient uzna, że przedstawione analizy wskazują na opłacalność tworzenia systemu przez wybrany zespół następuje ostateczne podpisanie kontraktu i rozpoczęcie właściwych prac nad systemem.
Założenia upraszczające#
Celem dalszej części pracy będzie wykazanie, że korzyści z proponowanego przez “Extreme Programming” modelu są obustronne, zapewniając klientowi dostarczenie większej wartości niż analogiczny projekt realizowany w oparciu o model klasyczny. Przeprowadzona analiza będzie miała charakter ekonomicznej oceny efektywności praktyk związanych ze współpracą z klientem (dostarczanie systemu we fragmentach, zasada szybkiej implementacji najbardziej wartościowych funkcji czy odwlekanie decyzji o kontynuacji prac), nie będzie natomiast starała się porównywać efektywności pracy samego zespołu. Dlatego też uzasadnione jest przyjęcie następujących założeń upraszczających:
- Końcowy produkt wytworzony przy użyciu obu modeli jest taki sam, co oznacza, że jego wartość dla klienta w momencie oddania do użytku jest taka sama. Nierealistycznie zaniedbujemy więc wartość dokumentacji wytworzonej w modelu klasycznym.
- W przypadku dostarczania systemu we fragmentach suma wartości fragmentów jest równa wartości całości.
- Okres czasu między realizacją kolejnych wersji systemu jest stały (jest to zalecenie twórców metodyki XP).
- Opłaty za realizację kolejnych wersji są stałe, co odpowiada założeniu, że suma kontraktu ma pokryć (z zyskiem) koszty związane z pracą zespołu. Koszty te w niewielkim stopniu zależą od zaawansowania prac ze względu na stały skład zespołu i unikanie nadgodzin.
- Koszt pozyskanie kapitału dla klienta jest stały dla obu metod i odpowiada ryzyku związanemu z projektem. Wynika to z faktu, że im większe ryzyko tym większy zwrot musi zapewniać inwestycja aby nadal była równie atrakcyjna. Wyraża to metoda CAPM [4] (model wyceny aktywów kapitałowych) zgodnie z którą koszt kapitału akcyjnego jest równy stopie wolnej od ryzyka zwiększonej o premię za ryzyko. Zasadność stosowania modeli rynków kapitałowych dla projektów programistycznych wykazuje H.Erdogmus i M.La Barre w artykule Value of Commercial Software Development under Technology Risk [11].
Oczywiście założenia te w przypadku wielu projektów odbiegają od rzeczywistości, jednakże są one niezbędne do przeprowadzenia analizy. Dalsze prace nad ekonomiczną analizą metodyki XP powinny więc zmierzać do rewizji przyjętych założeń i zastąpienia ich założeniami lepiej opisującymi rzeczywistość.
Analiza opłacalności podziału systemu na fragmenty#
W celu oceny wartości projektu dla klienta użyta zostanie szeroko stosowana metoda wartości zaktualizowanej netto NPV. Dzięki niej możliwe jest porównanie strumieni pieniężnych występujących w różnych okresach uwzględniając wartość pieniądza w czasie (pieniądz dziś jest wart więcej niż ta sama kwota w przyszłości). Wartość projektu będzie więc sumą zaktualizowanych wartości przyszłych dochodów i nakładów.Rozkład strumieni pieniężnych z punktu widzenia klienta (zapłata dopiero po otrzymaniu produktu) w metodyce XP i modelu klasycznym przedstawione są na rysunku 2 [5].
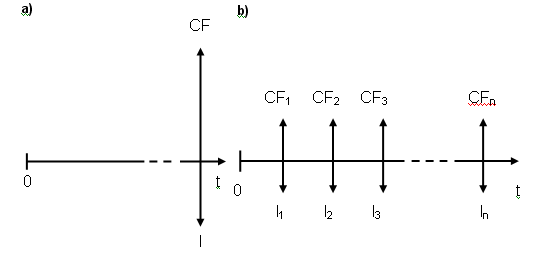
W modelu klasycznym bieżąca wartość inwestycji wynosi:
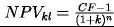
gdzie: CF – strumień pieniężny spodziewany po zrealizowaniu całości systemu obrazujący korzyści z jego użytkowania przez cały okres jego życia I – nakład inwestycyjny wymagany do zrealizowania systemu (suma kontraktu wpłacana po dostarczeniu produktu)
W przypadku metodyki XP wartość projektu (NPVXP) wyrażona jest równaniem (2) [4]:
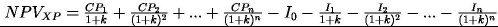
gdzie:
CFt – strumień pieniężny netto z wyłączeniem nakładów inwestycyjnych spodziewany w okresie t (t=1,2,…,n)
I0 – początkowy nakład inwestycyjny
It – nakład inwestycyjny wymagany w okresie t (t = 1,2,…,n)
k – stopa dyskonta, czyli koszt alternatywny zainwestowania kapitału w ryzykowne projekty (zależy on od ryzyka związanego z projektem)
n – czas “życia” projektu, a więc liczba okresów między decyzją o inwestycji a ostatnim strumieniem pieniężnym. Okres ten jest krótszy od długości życia systemu, gdyż przyjmujemy, że zdyskontowane korzyści z użytkowania wdrożonych funkcji są ujmowane w strumieniach pieniężnych z okresu w którym funkcje te zostały oddane klientowi.
Przyjmując równomierny rozkład inwestycji i przychodów, przychody i inwestycje we wszystkich okresach są takie same i wynoszą (patrz założenia upraszczające):
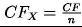
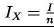
Wstawiając do (2) otrzymujemy:
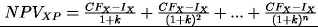
korzystając ze wzoru na aktualną wartość przyszłych seryjnych strumieni pieniężnych [3] oraz (3) i (4) uzyskujemy:
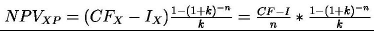
Do porównania otrzymanych wartości użyty zostanie ich iloraz, którego wartość większa od jedności wskazywać będzie na przewagę metodyki Extreme Programming (ogólnie modeli zakładających realizowanie fragmentów systemu – np. model spiralny lub przyrostowy).
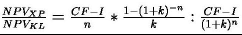
po prostych przekształceniach otrzymujemy:
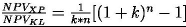
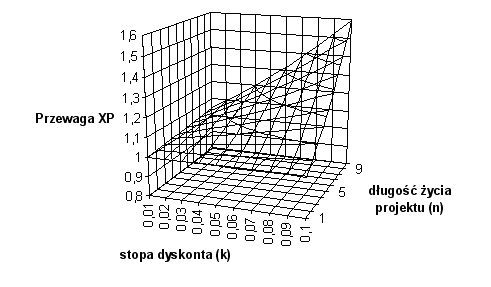
Wpływ k i n na jego wartość przedstawia wykres na rysunku 3, z którego jednoznacznie wynika, że przewaga metodyki Extreme Programming staje się szczególnie wyraźna dla projektów o dużym ryzyku. W takim to przypadku koszt pozyskania kapitału oraz oczekiwana stopa zwrotu z inwestycji jest na tyle wysoka, że każde odwlekanie wypuszczenia kolejnej wersji staje się bardzo kosztowne. Także liczba wersji ma ogromne znaczenia dla wartości z punktu widzenia klienta. Duża ich liczba a co za tym idzie szybkie otrzymanie pierwszej wersji produktu umożliwia natychmiastowe osiąganie zysków i zdobywanie rynku. Jest to bardzo istotne przede wszystkim w firmach “nowej gospodarki”, gdyż możliwości przyszłych przychodów zależą właśnie od błyskawicznej implementacji nowego pomysłu oraz jak najszybszego wyprzedzenia konkurencji.
Efekty szybkiej implementacji funkcji o największej wartości#
Przyjęte w poprzednim punkcie założenie o równomiernym rozłożeniu korzyści dla klienta w czasie, potrzebne było do wyizolowania wpływu podziału systemu na fragmenty, w rzeczywistości nie jest ono jednak prawdziwe. Fakt ten przedstawiony został na załączonym wykresie (rysunek 4) [8]. Wynika z niego, że różne funkcje systemu przedstawiają dla klienta bardzo zróżnicowane wartości, co po uwzględnieniu kosztów budowy oznaczać może nawet ujemne przepływy pieniężne w pierwszej fazie projektu.
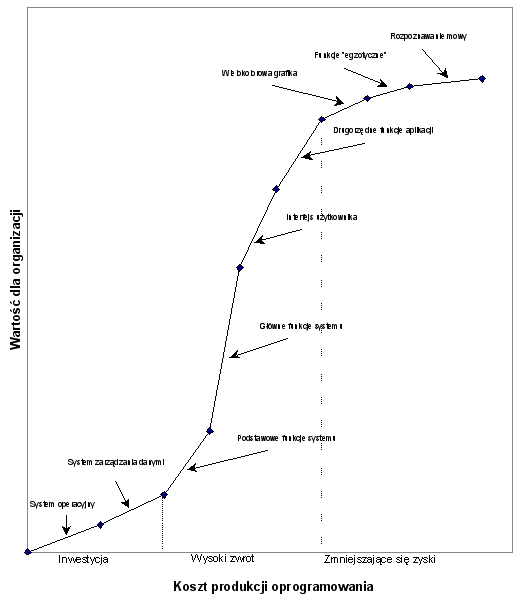
Najbardziej wartościowe są główne funkcje systemu i interfejs użytkownika, dlatego też metodyka XP zaleca ich jak najszybszą implementację. Oczywiście nie jest to możliwe bez zbudowania potrzebnych do tego funkcji elementarnych, takich jak współpraca z systemem operacyjnym czy system zarządzania danymi, co następuje już na etapie pierwszej wersji systemu. Do porównania wpływu szybkiej implementacji najbardziej wartościowych funkcji na zaktualizowaną wartość netto projektu pominięty zostanie wpływ tego okresu inwestycji, gdyż dla dowolnej metody implementacji etap ten zawsze występuje i nie może być pominięty – nie wpływa on więc na korzyści wynikające z wyboru strategii budowy systemu. Analiza porównawcza będzie dotyczyła metodyki XP a więc szybkiego dostarczenia najważniejszych funkcji oraz strategii zapewniającej równomierne rozłożenie korzyści dla klienta. Dla wyizolowania wpływu kolejności funkcji na wartość systemu przyjmujemy, że strategia porównawcza także charakteryzuje się iteracyjnością realizacji oprogramowania.Uchylając założenie o równomiernym rozłożeniu korzyści oraz pomijając początkowy okres inwestycji w funkcje elementarne, rozkład strumieni pieniężnych w czasie pokazany jest na rysunku 5 [5].
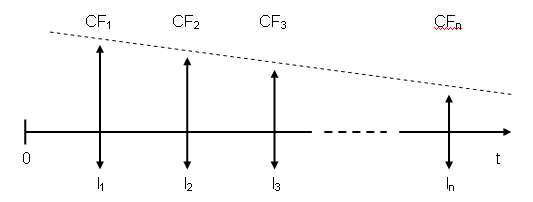
Zakładając liniową zależność wielkości strumieni pieniężnych od czasu, możemy obliczyć produkt krańcowy
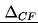
przypadający na kolejne wersje [14]:
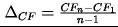
Odzwierciedla on szybkość spadku dostarczanej każdorazowo wartości wraz z postępem prac
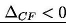
)
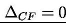
oznacza natomiast równomierne rozłożenie korzyści dla klienta. Kolejne strumienie pieniężne i zaktualizowana wartość projektu netto zależą od produktu krańcowego w następujący sposób:
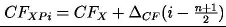
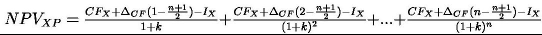
podczas gdy przy równomiernym rozłożeniu korzyści
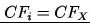
:
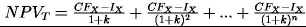
Jako miarę przewagi metodyki XP nad metodyką testową przyjęto przyrost zaktualizowanej wartości projektu netto wynikający z szybkiej implementacji najbardziej wartościowych funkcji:

po podstawieniu za
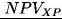
i
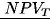
uzyskujemy:
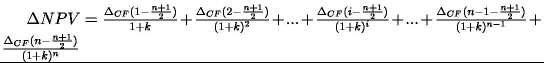
Zależność wielkości przyrostu wartości projektu od liczby iteracji i współczynnika dyskontującego k przedstawiono na rys. 6. Przy obliczaniu wartości
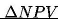
założono, że
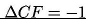
. Badanie zależności od tego jednostkowego przyrostu nie ma jednak uzasadnienia ze względu na jego liniową zależność bezpośrednio wynikającą z równania (14).
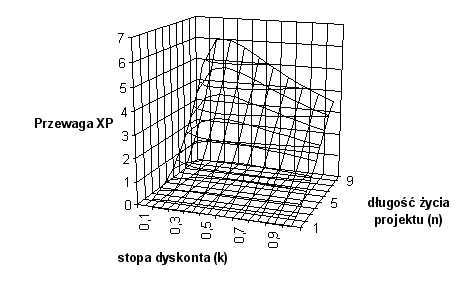
Wpływ poszczególnych zmiennych na wartość projektu jest więc następujący:
- Im większa liczba iteracji projektu – n, tym większe korzyści możliwe do osiągnięcia dzięki szybkiej implementacji funkcji o największej wartości. Zależność ta jest niemal liniowa.
- Wpływ współczynnika dyskontującego – k jest niejednoznaczny. Biorąc jednak pod uwagę, że jego wartość w rzeczywistości na ogół nie przekracza 0,4 zależność ta jest również dodatnia w rozsądnym przedziale.
Jak to już zostało zauważone, im większe są różnice w wartościach poszczególnych funkcji (
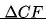
) tym większe potencjalne zyski.
Wartość elastyczności procesu produkcji#
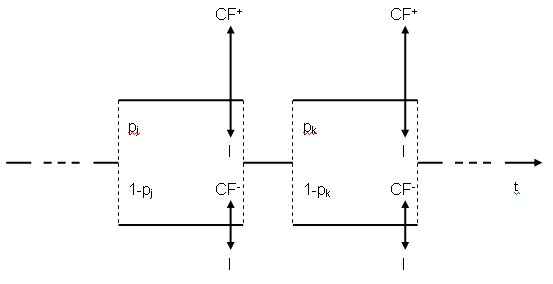
W dotychczasowych rozważaniach przyjęto, że rozkład korzyści z systemu, związany z użytkowaniem go przez klienta, nie zależy od zmian w otoczeniu i czynników losowych. W rzeczywistości jednak zdarza się, że określona funkcja na skutek zmian w warunkach zewnętrznych przestaje przedstawiać jakąkolwiek wartość. Metodyka XP umożliwia bieżącą kontrolę użyteczności wdrażanych funkcji i zapobieganie implementacji niepotrzebnych, lecz kosztownych modułów poprzez rozwinięty system planowania i ścisłą współpracę z klientem.Schematycznie wpływ zmian w otoczeniu na wartość poszczególnych wersji przedstawiono na rysunku 7 [5], na którym przyjęto następujące oznaczenia:
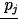
,
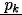
– prawdopodobieństwo, że wersja j (k) będzie miała dużą wartość dla klienta (sprzyjające warunki, wymagania klienta się nie zmieniają)
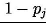
,
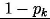
– prawdopodobieństwo, że wersja j (k) przestanie być wartościowa (niekorzystna zmiana otoczenia lub zmiana wymagań klienta) I – nakłady potrzebne na wyprodukowanie wersji – stałe wynagrodzenie dla firmy programistycznej
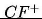
– aktualna wartość wersji w przypadku sprzyjających warunków
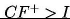
)
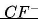
– aktualna wartość wersji w przypadku niesprzyjających warunków

Przy jednorazowym ustaleniu składu całego systemu oczekiwana aktualna wartość wersji w momencie rozpoczęcia jej tworzenia może być opisana w następujący sposób:
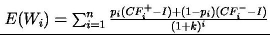
gdzie:
k – stopa dyskonta,
n – liczba iteracji.
W przypadku metodyki XP występuje dostosowywanie się do zmian w otoczeniu, można bowiem wybrać skład wersji gdy znamy już rzeczywiste warunki. Jeżeli oceniamy, że dana wersja przyniesie nam wzrost wartości netto projektu podejmujemy ją, natomiast w przeciwnym przypadku z niej rezygnujemy. W literaturze [7] [11] taką sytuację analizuje się za pomocą analizy typu “real options”. Polega ona na wycenieniu prawa (nie jest to zobowiązanie) do zakupu ryzykownego aktywu (tu: kolejna wersja) w przyszłości. Cena jaką płacimy za możliwość zrealizowania tej opcji to koszt budowy wersji. Rozumowanie to wywodzi się z modelu wyceny opcji finansowych, natomiast analityczne rozwiązanie tego zagadnienia dostarczyli trzej laureaci nagrody Nobla: Black, Scholes i Merton. Przybliżenie tej wartości daje model dwumianowy [12]:
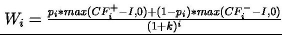
Przy założeniu, że
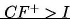

otrzymujemy:
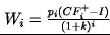
Wartość całego projektu jest więc następująca:
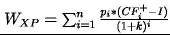
Przewagę metodyki XP można wyrazić poprzez iloraz wartości odpowiadających sobie projektów:
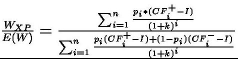
Zakładając, że rozkład prawdopodobieństw i wypłat we wszystkich okresach jest równy, otrzymujemy:
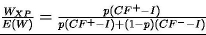
Zależność korzyści ze stosowania metodyki XP od prawdopodobieństwa zaistnienia korzystnych warunków oraz potencjalnej wysokości strat przedstawiono na rysunku 8. Dla uproszczenia założono, że zysk firmy (
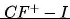
) wynosi jeden.
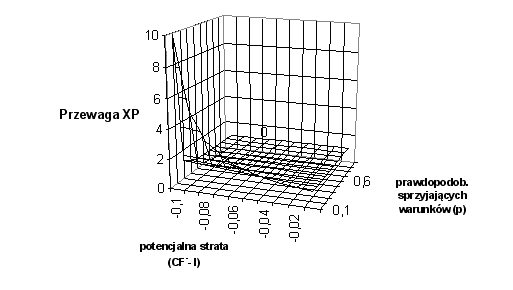
Przewaga XP wzrasta więc wraz ze spadkiem prawdopodobieństwa sprzyjających warunków (ryzykowne przedsięwzięcie) oraz ze wzrostem ewentualnych przyszłych strat (niekorzystne warunki w dużym stopniu obniżą wartość wersji).
Zakończenie#
Metodyka “Extreme Programming” stanowi wyjątkowo efektywne połączenie wielu różnych praktyk uzyskując dzięki temu różnorodne efekty synergii. Jak widać z przeprowadzonej analizy do najważniejszych czynników wpływających na wysoką efektywność badanej metodyki należy cykliczność dostarczania kolejnych fragmentów systemu. Wynikające z niej korzyści zwiększają się wraz ze wzrostem kosztu pozyskania kapitału oraz zróżnicowania wartości kolejnych wersji. Dodatkowym czynnikiem przewagi metodyki XP jest również możliwość opóźnienia decyzji o kontynuacji prac nad systemem do momentu uzyskania pełniejszych informacji o warunkach zewnętrznych. Ma to szczególnie duże znaczenie w przypadku projektów narażonych na duże ryzyko zmiany otoczenia lub wymogów klienta. Do wyników tych doprowadziły nas jednak rygorystyczne założenia upraszczające, co powoduje konieczność dalszych badań celem lepszego odzwierciedlenia rzeczywistości.Podsumowując należy stwierdzić, że “Extreme Programming” stanowi niezwykle efektywną metodykę tworzenia systemów informatycznych, która jest jednak ograniczona do dość wąskiego typu oprogramowania: małe niezbyt skomplikowane systemy tworzone przez niewielkie zespoły. Dodatkowo należy upewnić się, że klient nie planuje w przyszłości radykalnej rozbudowy oraz, że nie potrzebuje rozbudowanej dokumentacji. Jeżeli warunki te zostaną spełnione, firma programistyczna może wyprodukować dobry jakościowo system zgodny z oczekiwaniami klienta w krótkim czasie. Korzyści z tej decyzji staną się jeszcze wyraźniejsze w przypadku zmiennego otoczenia oraz dużego ryzyka z tym związanego.
Bibliografia#
| [1] | K. Beck i D. Cleal, Optional Scope Contracts, 1999. |
| [2] | K. Beck, Wydajne programowanie, 2001, Mikom. |
| [3] | W. Bień, Zarządzanie finansami w przedsiębiorstwie, 2000, Difin. |
| [4] | E. Brigham i L. Gapenski, Zarządzanie finansami, 2000, PWE. |
| [5] | K. Górbiel, Ocena Efektywności Metodyki Extreme Programming, 2001, Szkoła Główna Handlowa, Warszawa. |
| [6] | URL: http://extremeprogramming.org/Project.vpp. |
| [7] | M. Benaroch i R. Kauffman, A Case for Using Real Options Pricing Analysis to Evaluate Information Technology Project Investments.,http://sominfo.syr.edu/facstaff/mbenaroc/resume/PAPERS/OPM-ISR/WWW-PAPR.html. |
| [8] | P. K. Hoh, Software Engineering Economics – materiały do kursu: (B.Boehm, Software Engineering Economics)., http://www.comp.nus.edu.sg/~phuakh/chapters3\ &4.ppt, slajd nr 52. |
| [10] | C. , XP Distilled, http://www-106.ibm.com/developerworks/java/library/j-xp/. |
| [11] | H. Erdogmus, Value of Commercial Software Development under Technology Risk, http://wwwsel.iit.nrc.ca/~erdogmus/papers/SE-Economics/ISJ00.pdf. |
| [12] | H. Erdogmus i J. Vandergraaf, The Binomial Option Pricing Model, http://wwwsel.iit.nrc.ca/~erdogmus/SIA/Binomial/BinomialOPM.html. |
| [13] | A. Jaszkiewicz, Inżynieria Oprogramowania, 1997, Helion. |
| [14] | H. Varian, Mikroekonomia, 1995, PWN. |








